# 图解快速diff
>面试题:讲一讲 Vue3 的 diff 算法做了哪些改变?
**双端存在的问题**
在 Vue2 的双端 diff 中,主要的步骤如下:
1. 新头和旧头比较
2. 新尾和旧尾比较
3. 旧头和新尾比较
4. 新头和旧尾比较
5. 暴力对比
这种对比策略其实会存在**额外的移动操作**。
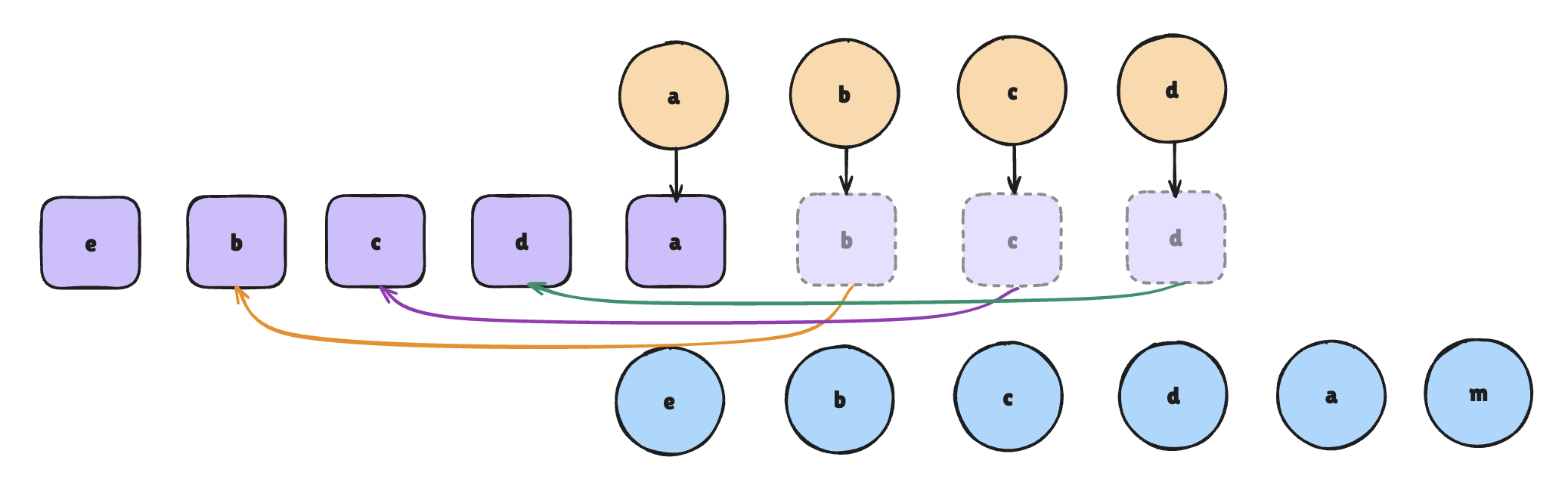 - 对于 e 节点匹配不到,新建 e 节点对应的 DOM 节点,放置于旧头对应的 DOM 节点的前面
- 对于 b 节点,通过暴力比对能够找到,将 b 节点移动到旧头对应的 DOM 节点的前面
- 依此类推,c 节点、d 节点所对应的 DOM 节点都会进行移动操作
问题:其实完全不需要移动 bcd 节点,因为在新旧列表里面,这几个节点的顺序是一致的。只需要将 a 节点对应的 DOM 移动到 d 节点后即可。
**Vue3快速diff**
1. 头头比对
2. 尾尾比对
3. 非复杂情况处理
4. 复杂情况处理
**和双端相同步骤**
1. 头头比对
2. 尾尾比对
3. 非复杂情况:指的是经历了头头比对和尾尾比对后,新旧列表有任意一方结束,此时会存在两种情况:
- 旧节点列表有剩余:对应的旧 DOM 节点全部删除
- 新节点列表有剩余:创建对应的 DOM 节点,放置于新头节点对应的 DOM 节点之后
**和双端不同的步骤**
经历了头头比对,尾尾比对后,新旧节点列表都有剩余,之后的步骤就和双端 diff 不一样:
1. 初始化keyToNewIndexMap
2. 初始化newIndexToOldIndexMap
3. 更新newIndexToOldIndexMap
4. 计算最长递增子序列
5. 移动和挂载节点
**1. 初始化keyToNewIndexMap**
首先,定义了一个用于保存新节点下标的容器 keyToNewIndexMap,它的形式是 key - index,遍历还未处理的新节点,将它们的key和下标的映射关系存储到 keyToNewIndexMap 中。
```js
const keyToNewIndexMap = new Map();
for (let i = newStartIdx; i <= newEndIdx; i++) {
const key = newChildren[i].key;
keyToNewIndexMap.set(key, i);
}
```
示意图:
- 对于 e 节点匹配不到,新建 e 节点对应的 DOM 节点,放置于旧头对应的 DOM 节点的前面
- 对于 b 节点,通过暴力比对能够找到,将 b 节点移动到旧头对应的 DOM 节点的前面
- 依此类推,c 节点、d 节点所对应的 DOM 节点都会进行移动操作
问题:其实完全不需要移动 bcd 节点,因为在新旧列表里面,这几个节点的顺序是一致的。只需要将 a 节点对应的 DOM 移动到 d 节点后即可。
**Vue3快速diff**
1. 头头比对
2. 尾尾比对
3. 非复杂情况处理
4. 复杂情况处理
**和双端相同步骤**
1. 头头比对
2. 尾尾比对
3. 非复杂情况:指的是经历了头头比对和尾尾比对后,新旧列表有任意一方结束,此时会存在两种情况:
- 旧节点列表有剩余:对应的旧 DOM 节点全部删除
- 新节点列表有剩余:创建对应的 DOM 节点,放置于新头节点对应的 DOM 节点之后
**和双端不同的步骤**
经历了头头比对,尾尾比对后,新旧节点列表都有剩余,之后的步骤就和双端 diff 不一样:
1. 初始化keyToNewIndexMap
2. 初始化newIndexToOldIndexMap
3. 更新newIndexToOldIndexMap
4. 计算最长递增子序列
5. 移动和挂载节点
**1. 初始化keyToNewIndexMap**
首先,定义了一个用于保存新节点下标的容器 keyToNewIndexMap,它的形式是 key - index,遍历还未处理的新节点,将它们的key和下标的映射关系存储到 keyToNewIndexMap 中。
```js
const keyToNewIndexMap = new Map();
for (let i = newStartIdx; i <= newEndIdx; i++) {
const key = newChildren[i].key;
keyToNewIndexMap.set(key, i);
}
```
示意图:
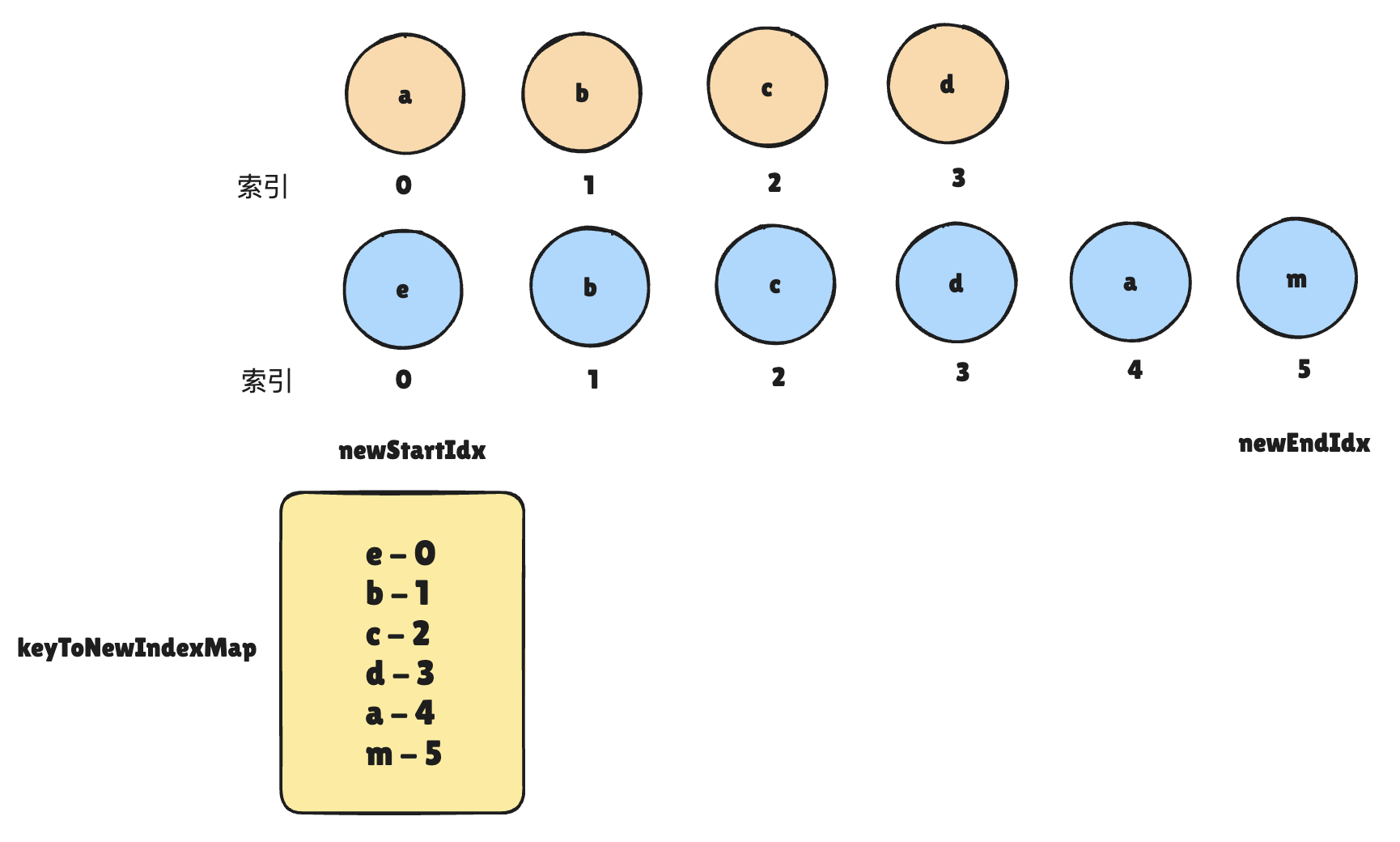 也就是说,该 map 存储了所有未处理的新节点的 key 和 index 的映射关系。
**2. 初始化newIndexToOldIndexMap**
然后,定义了一个和未处理新节点个数同样大小的数组**newIndexToOldIndexMap**,默认每一项均为 0
```js
const toBePatched = newEndIdx - newStartIdx + 1; // 计算没有处理的新节点的个数
const newIndexToOldIndexMap = new Array(toBePatched).fill(0);
```
示意图:
也就是说,该 map 存储了所有未处理的新节点的 key 和 index 的映射关系。
**2. 初始化newIndexToOldIndexMap**
然后,定义了一个和未处理新节点个数同样大小的数组**newIndexToOldIndexMap**,默认每一项均为 0
```js
const toBePatched = newEndIdx - newStartIdx + 1; // 计算没有处理的新节点的个数
const newIndexToOldIndexMap = new Array(toBePatched).fill(0);
```
示意图:
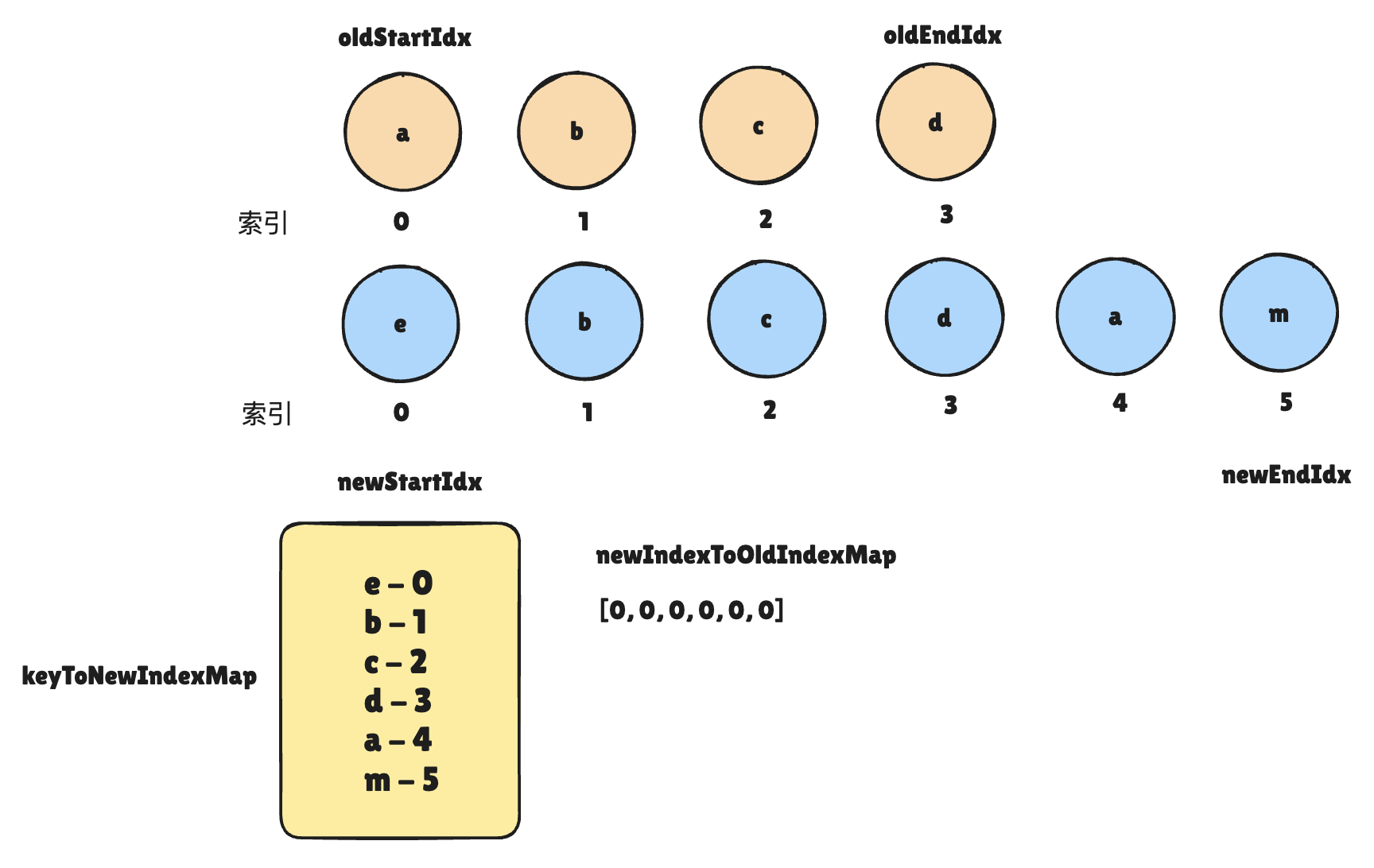 之所以一开始初始化为 0 ,其实是为了一开始假设新节点不存在于旧节点列表,之后就会对这个数组进行更新,倘若更新之后当前某个位置还为 0 ,就代表这一位对应的新节点在旧节点列表中不存在。
**3. 更新newIndexToOldIndexMap**
遍历未处理的**旧节点**,查找旧节点在新节点中的位置,决定是更新、删除还是移动。
- 遍历未处理的旧节点(从 oldStartIdx 到 oldEndIdx)
- 对于每个旧节点,执行以下操作:
- 查找对应的新节点索引 newIndex:
- 如果旧节点有 key,通过 keyToNewIndexMap 获取 newIndex
- 如果没有 key,需要遍历新节点列表,找到第一个与旧节点相同的节点
- 判断节点是否存在与新节点列表:
- 如果 newIndex 没有找到,说明旧节点已经被删除,需要卸载
- 如果 newIndex 找到,说明节点需要保留,执行以下操作:
- 更新节点:调用 patch 函数更新节点内容
- 记录映射关系:将旧节点的索引 +1 记录到 `newIndexToOldIndexMap[newIndex - newStartIdx]` 中
>思考🤔:为什么要把旧节点的索引 +1 然后进行存储?
>
>答案:因为前面我们在初始化newIndexToOldIndexMap这个数组的时候,所有的值都初始化为了0,代表新节点在旧节点列表中不存在。如果直接存储旧节点的索引,而恰好这个旧节点的索引又为0,那么此时是无法区分究竟是索引值还是不存在。
- 标记节点是否需要移动:通过比较当前的遍历顺序和 newIndex,初步判断节点是否需要移动。
示意代码:
```js
let moved = false;
let maxNewIndexSoFar = 0;
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
const oldNode = oldChildren[i];
let newIndex;
if (oldNode.key != null) {
// 旧节点存在 key,根据 key 找到该节点在新节点列表里面的索引值
newIndex = keyToNewIndexMap.get(oldNode.key);
} else {
// 遍历新节点列表匹配
}
if (newIndex === undefined) {
// 旧节点在新节点中不存在,卸载
} else {
// 更新节点
patch(oldNode, newChildren[newIndex], container);
// 记录映射关系,注意这里在记录的时候,旧节点的索引要加1
newIndexToOldIndexMap[newIndex - newStartIdx] = i + 1;
// 判断是否需要移动
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
}
}
```
详细步骤:
- i = 0:`[0, 0, 0, 0, 1, 0]`
- i = 1:`[0, 2, 0, 0, 1, 0]`
- i = 2:`[0, 2, 3, 0, 1, 0]`
- i = 3::`[0, 2, 3, 4, 1, 0]`
之所以一开始初始化为 0 ,其实是为了一开始假设新节点不存在于旧节点列表,之后就会对这个数组进行更新,倘若更新之后当前某个位置还为 0 ,就代表这一位对应的新节点在旧节点列表中不存在。
**3. 更新newIndexToOldIndexMap**
遍历未处理的**旧节点**,查找旧节点在新节点中的位置,决定是更新、删除还是移动。
- 遍历未处理的旧节点(从 oldStartIdx 到 oldEndIdx)
- 对于每个旧节点,执行以下操作:
- 查找对应的新节点索引 newIndex:
- 如果旧节点有 key,通过 keyToNewIndexMap 获取 newIndex
- 如果没有 key,需要遍历新节点列表,找到第一个与旧节点相同的节点
- 判断节点是否存在与新节点列表:
- 如果 newIndex 没有找到,说明旧节点已经被删除,需要卸载
- 如果 newIndex 找到,说明节点需要保留,执行以下操作:
- 更新节点:调用 patch 函数更新节点内容
- 记录映射关系:将旧节点的索引 +1 记录到 `newIndexToOldIndexMap[newIndex - newStartIdx]` 中
>思考🤔:为什么要把旧节点的索引 +1 然后进行存储?
>
>答案:因为前面我们在初始化newIndexToOldIndexMap这个数组的时候,所有的值都初始化为了0,代表新节点在旧节点列表中不存在。如果直接存储旧节点的索引,而恰好这个旧节点的索引又为0,那么此时是无法区分究竟是索引值还是不存在。
- 标记节点是否需要移动:通过比较当前的遍历顺序和 newIndex,初步判断节点是否需要移动。
示意代码:
```js
let moved = false;
let maxNewIndexSoFar = 0;
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
const oldNode = oldChildren[i];
let newIndex;
if (oldNode.key != null) {
// 旧节点存在 key,根据 key 找到该节点在新节点列表里面的索引值
newIndex = keyToNewIndexMap.get(oldNode.key);
} else {
// 遍历新节点列表匹配
}
if (newIndex === undefined) {
// 旧节点在新节点中不存在,卸载
} else {
// 更新节点
patch(oldNode, newChildren[newIndex], container);
// 记录映射关系,注意这里在记录的时候,旧节点的索引要加1
newIndexToOldIndexMap[newIndex - newStartIdx] = i + 1;
// 判断是否需要移动
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
}
}
```
详细步骤:
- i = 0:`[0, 0, 0, 0, 1, 0]`
- i = 1:`[0, 2, 0, 0, 1, 0]`
- i = 2:`[0, 2, 3, 0, 1, 0]`
- i = 3::`[0, 2, 3, 4, 1, 0]`
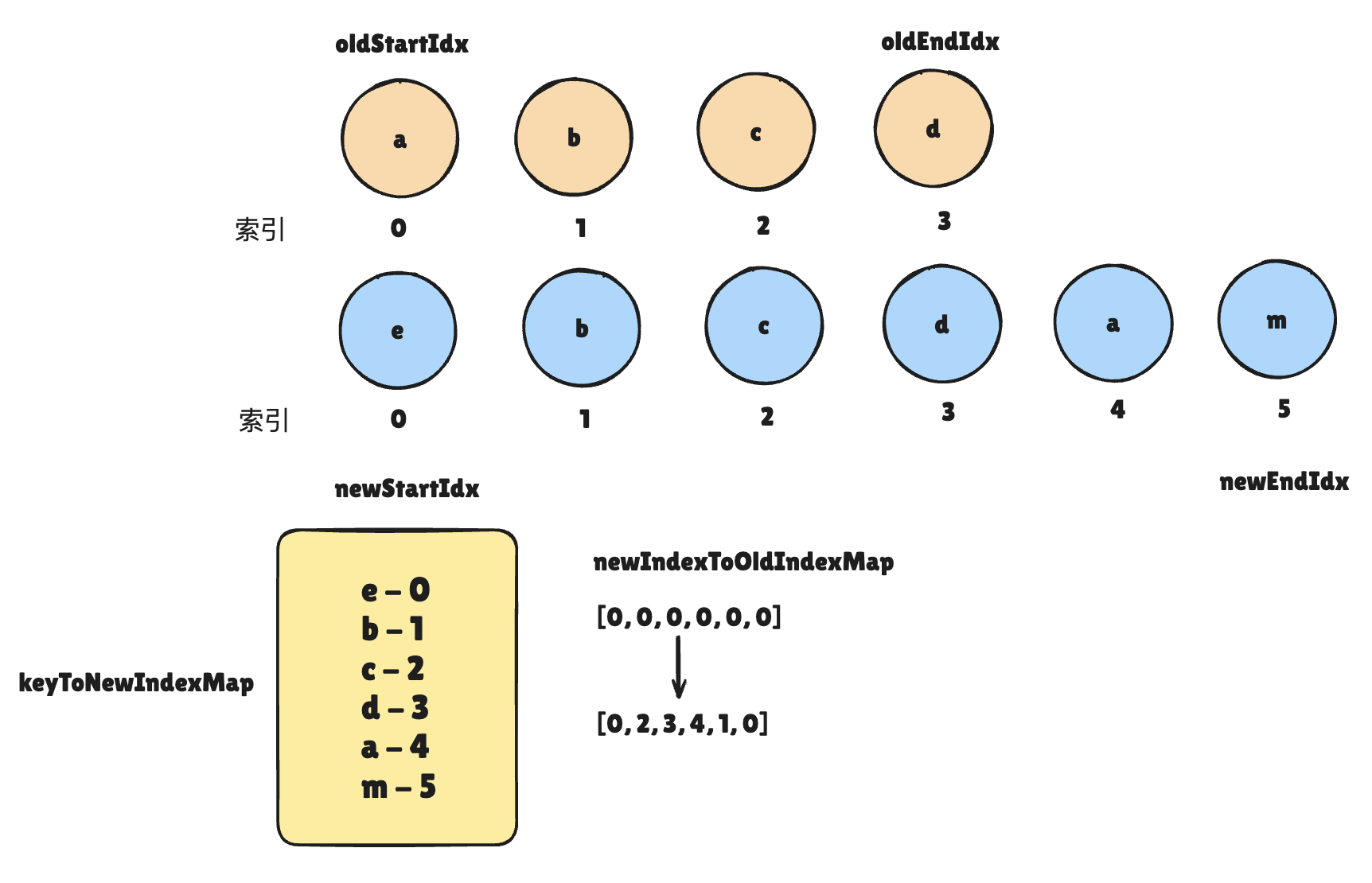 经过遍历旧节点列表这一操作之后,newIndexToOldIndexMap 就被更新,里面存储了每个新节点在旧节点列表里面的位置,不过要注意,这个索引位置是 +1. 更新后如果某一项仍然是 0,说明这一个节点确实在旧节点列表中不存在
```js
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
```
maxNewIndexSoFar 用于判断节点的相对顺序是否保持递增,以决定是否需要移动节点。
- 如果当前的新节点索引大于等于 maxNewIndexSoFar,更新 maxNewIndexSoFar,节点相对顺序正确,无需标记移动
- 如果小于,说明节点相对顺序发生变化,标记 moved = true,后续需要根据 LIS 决定是否移动节点。
**4. 计算最长递增子序列**
通过 LIS,确定哪些节点的相对顺序未变,减少需要移动的节点数量。如果在前面的步骤中标记了 moved = true,说明有节点需要移动。使用 newIndexToOldIndexMap 计算最长递增子序列 increasingNewIndexSequence.
```js
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : [];
```
上一步我们得到的 newIndexToOldIndex 为 `[0, 2, 3, 4, 1, 0]`,之后得到的最长递增子序列为 `[1, 2, 3]`,注意,Vue3内部在计算最长递增子序列的时候,返回的是元素对应的索引值。
思考🤔:注意这里的最长递增子序列不是记录的具体元素,而是元素对应的下标值。这样有什么好处?
答案:这样刚好抵消了前面+1的操作,重新变回了旧节点的下标。
**5. 移动和挂载节点**
根据计算结果,对需要移动和新建的节点进行处理。**倒序遍历**未处理的新节点。
思考🤔:为什么要倒序遍历?
答案:因为后续的节点位置是确定了的,通过倒序的方式能够避免锚点引用的时候不会出错。
具体步骤:
1. 计算当前新节点在新节点列表中的索引 newIndex = newStartIdx + i
- newStartIdx 是未处理节点的起始索引
- i 为倒序遍历时的索引值
2. 获取锚点 DOM,其目的是为了作为节点移动的参照物,当涉及到移动操作时,都移动到锚点 DOM 的前面
- 计算方法为 `newIndex + 1 < newChildren.length ? newChildren[newIndex + 1].el : null`
- 如果计算出来为 null,表示没有对应的锚点 DOM ,那么就创建并挂载到最后
3. 判断节点究竟是新挂载还是移动
- **判断节点是否需要挂载**:如果 `newIndexToOldIndexMap[i] === 0`,说明该节点在旧节点中不存在,需要创建并插入到锚点DOM位置之前。
```js
if (newIndexToOldIndexMap[i] === 0) {
// 创建新节点并插入到锚点DOM位置之前
patch(/*参数略 */);
}
```
- **判断节点是否需要移动**:如果节点在 increasingNewIndexSequence 中,说明位置正确,无需移动。如果不在,则需要移动节点到锚点DOM位置之前。
```js
else if (moved) {
if (!increasingNewIndexSequence.includes(i)) {
// 移动节点到锚点DOM之前
move(/*参数略 */);
}
}
```
详细步骤:
- i = 5
- newIndex = 5
- 锚点DOM:null
- 创建 m 对应的真实 DOM,挂载到最后
- i = 4
- newIndex = 4
- 锚点DOM:m --> 真实DOM
- `newIndexToOldIndexMap[4]` 是否为 0,不是说明在旧节点列表里面是有的,能够复用
- 接下来看 i 是否在最长递增子序列里面,发现没有在最长递增子序列里面,那么这里就涉及到移动,移动到锚点DOM的前面,也就是 m 前面
- i = 3
- newIndex = 3
- 锚点DOM:a --> 真实DOM
- `newIndexToOldIndexMap[3]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 2
- newIndex = 2
- 锚点DOM:d --> 真实DOM
- `newIndexToOldIndexMap[2]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 1
- newIndex = 1
- 锚点DOM:c --> 真实DOM
- `newIndexToOldIndexMap[1]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 0
- newIndex = 0
- 锚点DOM:b --> 真实DOM
- `newIndexToOldIndexMap[0]` 为0,说明旧节点列表里面没有
- 创建新的 DOM 节点,插入到锚点 DOM 节点之前
最终经过上面的操作:
1. e:新建并且插入到 b 之前
2. b: 位置不变,没有做移动操作
3. c:位置不变,没有做移动操作
4. d:位置不变,没有做移动操作
5. a:移动到 m 之前
6. m:新建并且插入到末尾
整个 diff 下来 DOM 操作仅仅有 1 次移动,2 次新建。做到了最最最小化 DOM 操作次数,没有一次 DOM 操作是多余的。
>面试题:讲一讲 Vue3 的 diff 算法做了哪些改变?
>
>参考答案:
>
>Vue2 采用的是双端 diff 算法,而 Vue3 采用的是快速 diff. 这两种 diff 算法前面的步骤都是相同的,先是新旧列表的头节点进行比较,当发现无法复用则进行新旧节点列表的尾节点比较。
>
>一头一尾比较完后,如果旧节点列表有剩余,就将对应的旧 DOM 节点全部删除掉,如果新节点列表有剩余:将新节点列表中剩余的节点创建对应的 DOM,放置于新头节点对应的 DOM 节点后面。
>
>之后两种 diff 算法呈现出不同的操作,双端会进行旧头新尾比较、无法复用则进行旧尾新头比较、再无法复用这是暴力比对,这样的处理会存在多余的移动操作,即便一些新节点的前后顺序和旧节点是一致的,但是还是会产生移动操作。
>
>而 Vue3 快速 diff 则采用了另外一种做法,找到新节点在旧节点中对应的索引列表,然后求出最长递增子序列,凡是位于最长递增子序列里面的索引所对应的元素,是不需要移动位置的,这就做到了只移动需要移动的 DOM 节点,最小化了 DOM 的操作次数,没有任何无意义的移动。可以这么说,Vue3 的 diff 再一次将性能优化到了极致,整套操作下来,没有一次 DOM 操作是多余的,仅仅执行了最必要的 DOM 操作。
---
-EOF-
经过遍历旧节点列表这一操作之后,newIndexToOldIndexMap 就被更新,里面存储了每个新节点在旧节点列表里面的位置,不过要注意,这个索引位置是 +1. 更新后如果某一项仍然是 0,说明这一个节点确实在旧节点列表中不存在
```js
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
```
maxNewIndexSoFar 用于判断节点的相对顺序是否保持递增,以决定是否需要移动节点。
- 如果当前的新节点索引大于等于 maxNewIndexSoFar,更新 maxNewIndexSoFar,节点相对顺序正确,无需标记移动
- 如果小于,说明节点相对顺序发生变化,标记 moved = true,后续需要根据 LIS 决定是否移动节点。
**4. 计算最长递增子序列**
通过 LIS,确定哪些节点的相对顺序未变,减少需要移动的节点数量。如果在前面的步骤中标记了 moved = true,说明有节点需要移动。使用 newIndexToOldIndexMap 计算最长递增子序列 increasingNewIndexSequence.
```js
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : [];
```
上一步我们得到的 newIndexToOldIndex 为 `[0, 2, 3, 4, 1, 0]`,之后得到的最长递增子序列为 `[1, 2, 3]`,注意,Vue3内部在计算最长递增子序列的时候,返回的是元素对应的索引值。
思考🤔:注意这里的最长递增子序列不是记录的具体元素,而是元素对应的下标值。这样有什么好处?
答案:这样刚好抵消了前面+1的操作,重新变回了旧节点的下标。
**5. 移动和挂载节点**
根据计算结果,对需要移动和新建的节点进行处理。**倒序遍历**未处理的新节点。
思考🤔:为什么要倒序遍历?
答案:因为后续的节点位置是确定了的,通过倒序的方式能够避免锚点引用的时候不会出错。
具体步骤:
1. 计算当前新节点在新节点列表中的索引 newIndex = newStartIdx + i
- newStartIdx 是未处理节点的起始索引
- i 为倒序遍历时的索引值
2. 获取锚点 DOM,其目的是为了作为节点移动的参照物,当涉及到移动操作时,都移动到锚点 DOM 的前面
- 计算方法为 `newIndex + 1 < newChildren.length ? newChildren[newIndex + 1].el : null`
- 如果计算出来为 null,表示没有对应的锚点 DOM ,那么就创建并挂载到最后
3. 判断节点究竟是新挂载还是移动
- **判断节点是否需要挂载**:如果 `newIndexToOldIndexMap[i] === 0`,说明该节点在旧节点中不存在,需要创建并插入到锚点DOM位置之前。
```js
if (newIndexToOldIndexMap[i] === 0) {
// 创建新节点并插入到锚点DOM位置之前
patch(/*参数略 */);
}
```
- **判断节点是否需要移动**:如果节点在 increasingNewIndexSequence 中,说明位置正确,无需移动。如果不在,则需要移动节点到锚点DOM位置之前。
```js
else if (moved) {
if (!increasingNewIndexSequence.includes(i)) {
// 移动节点到锚点DOM之前
move(/*参数略 */);
}
}
```
详细步骤:
- i = 5
- newIndex = 5
- 锚点DOM:null
- 创建 m 对应的真实 DOM,挂载到最后
- i = 4
- newIndex = 4
- 锚点DOM:m --> 真实DOM
- `newIndexToOldIndexMap[4]` 是否为 0,不是说明在旧节点列表里面是有的,能够复用
- 接下来看 i 是否在最长递增子序列里面,发现没有在最长递增子序列里面,那么这里就涉及到移动,移动到锚点DOM的前面,也就是 m 前面
- i = 3
- newIndex = 3
- 锚点DOM:a --> 真实DOM
- `newIndexToOldIndexMap[3]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 2
- newIndex = 2
- 锚点DOM:d --> 真实DOM
- `newIndexToOldIndexMap[2]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 1
- newIndex = 1
- 锚点DOM:c --> 真实DOM
- `newIndexToOldIndexMap[1]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 0
- newIndex = 0
- 锚点DOM:b --> 真实DOM
- `newIndexToOldIndexMap[0]` 为0,说明旧节点列表里面没有
- 创建新的 DOM 节点,插入到锚点 DOM 节点之前
最终经过上面的操作:
1. e:新建并且插入到 b 之前
2. b: 位置不变,没有做移动操作
3. c:位置不变,没有做移动操作
4. d:位置不变,没有做移动操作
5. a:移动到 m 之前
6. m:新建并且插入到末尾
整个 diff 下来 DOM 操作仅仅有 1 次移动,2 次新建。做到了最最最小化 DOM 操作次数,没有一次 DOM 操作是多余的。
>面试题:讲一讲 Vue3 的 diff 算法做了哪些改变?
>
>参考答案:
>
>Vue2 采用的是双端 diff 算法,而 Vue3 采用的是快速 diff. 这两种 diff 算法前面的步骤都是相同的,先是新旧列表的头节点进行比较,当发现无法复用则进行新旧节点列表的尾节点比较。
>
>一头一尾比较完后,如果旧节点列表有剩余,就将对应的旧 DOM 节点全部删除掉,如果新节点列表有剩余:将新节点列表中剩余的节点创建对应的 DOM,放置于新头节点对应的 DOM 节点后面。
>
>之后两种 diff 算法呈现出不同的操作,双端会进行旧头新尾比较、无法复用则进行旧尾新头比较、再无法复用这是暴力比对,这样的处理会存在多余的移动操作,即便一些新节点的前后顺序和旧节点是一致的,但是还是会产生移动操作。
>
>而 Vue3 快速 diff 则采用了另外一种做法,找到新节点在旧节点中对应的索引列表,然后求出最长递增子序列,凡是位于最长递增子序列里面的索引所对应的元素,是不需要移动位置的,这就做到了只移动需要移动的 DOM 节点,最小化了 DOM 的操作次数,没有任何无意义的移动。可以这么说,Vue3 的 diff 再一次将性能优化到了极致,整套操作下来,没有一次 DOM 操作是多余的,仅仅执行了最必要的 DOM 操作。
---
-EOF- - 对于 e 节点匹配不到,新建 e 节点对应的 DOM 节点,放置于旧头对应的 DOM 节点的前面
- 对于 b 节点,通过暴力比对能够找到,将 b 节点移动到旧头对应的 DOM 节点的前面
- 依此类推,c 节点、d 节点所对应的 DOM 节点都会进行移动操作
问题:其实完全不需要移动 bcd 节点,因为在新旧列表里面,这几个节点的顺序是一致的。只需要将 a 节点对应的 DOM 移动到 d 节点后即可。
**Vue3快速diff**
1. 头头比对
2. 尾尾比对
3. 非复杂情况处理
4. 复杂情况处理
**和双端相同步骤**
1. 头头比对
2. 尾尾比对
3. 非复杂情况:指的是经历了头头比对和尾尾比对后,新旧列表有任意一方结束,此时会存在两种情况:
- 旧节点列表有剩余:对应的旧 DOM 节点全部删除
- 新节点列表有剩余:创建对应的 DOM 节点,放置于新头节点对应的 DOM 节点之后
**和双端不同的步骤**
经历了头头比对,尾尾比对后,新旧节点列表都有剩余,之后的步骤就和双端 diff 不一样:
1. 初始化keyToNewIndexMap
2. 初始化newIndexToOldIndexMap
3. 更新newIndexToOldIndexMap
4. 计算最长递增子序列
5. 移动和挂载节点
**1. 初始化keyToNewIndexMap**
首先,定义了一个用于保存新节点下标的容器 keyToNewIndexMap,它的形式是 key - index,遍历还未处理的新节点,将它们的key和下标的映射关系存储到 keyToNewIndexMap 中。
```js
const keyToNewIndexMap = new Map();
for (let i = newStartIdx; i <= newEndIdx; i++) {
const key = newChildren[i].key;
keyToNewIndexMap.set(key, i);
}
```
示意图:
- 对于 e 节点匹配不到,新建 e 节点对应的 DOM 节点,放置于旧头对应的 DOM 节点的前面
- 对于 b 节点,通过暴力比对能够找到,将 b 节点移动到旧头对应的 DOM 节点的前面
- 依此类推,c 节点、d 节点所对应的 DOM 节点都会进行移动操作
问题:其实完全不需要移动 bcd 节点,因为在新旧列表里面,这几个节点的顺序是一致的。只需要将 a 节点对应的 DOM 移动到 d 节点后即可。
**Vue3快速diff**
1. 头头比对
2. 尾尾比对
3. 非复杂情况处理
4. 复杂情况处理
**和双端相同步骤**
1. 头头比对
2. 尾尾比对
3. 非复杂情况:指的是经历了头头比对和尾尾比对后,新旧列表有任意一方结束,此时会存在两种情况:
- 旧节点列表有剩余:对应的旧 DOM 节点全部删除
- 新节点列表有剩余:创建对应的 DOM 节点,放置于新头节点对应的 DOM 节点之后
**和双端不同的步骤**
经历了头头比对,尾尾比对后,新旧节点列表都有剩余,之后的步骤就和双端 diff 不一样:
1. 初始化keyToNewIndexMap
2. 初始化newIndexToOldIndexMap
3. 更新newIndexToOldIndexMap
4. 计算最长递增子序列
5. 移动和挂载节点
**1. 初始化keyToNewIndexMap**
首先,定义了一个用于保存新节点下标的容器 keyToNewIndexMap,它的形式是 key - index,遍历还未处理的新节点,将它们的key和下标的映射关系存储到 keyToNewIndexMap 中。
```js
const keyToNewIndexMap = new Map();
for (let i = newStartIdx; i <= newEndIdx; i++) {
const key = newChildren[i].key;
keyToNewIndexMap.set(key, i);
}
```
示意图:
 也就是说,该 map 存储了所有未处理的新节点的 key 和 index 的映射关系。
**2. 初始化newIndexToOldIndexMap**
然后,定义了一个和未处理新节点个数同样大小的数组**newIndexToOldIndexMap**,默认每一项均为 0
```js
const toBePatched = newEndIdx - newStartIdx + 1; // 计算没有处理的新节点的个数
const newIndexToOldIndexMap = new Array(toBePatched).fill(0);
```
示意图:
也就是说,该 map 存储了所有未处理的新节点的 key 和 index 的映射关系。
**2. 初始化newIndexToOldIndexMap**
然后,定义了一个和未处理新节点个数同样大小的数组**newIndexToOldIndexMap**,默认每一项均为 0
```js
const toBePatched = newEndIdx - newStartIdx + 1; // 计算没有处理的新节点的个数
const newIndexToOldIndexMap = new Array(toBePatched).fill(0);
```
示意图:
 之所以一开始初始化为 0 ,其实是为了一开始假设新节点不存在于旧节点列表,之后就会对这个数组进行更新,倘若更新之后当前某个位置还为 0 ,就代表这一位对应的新节点在旧节点列表中不存在。
**3. 更新newIndexToOldIndexMap**
遍历未处理的**旧节点**,查找旧节点在新节点中的位置,决定是更新、删除还是移动。
- 遍历未处理的旧节点(从 oldStartIdx 到 oldEndIdx)
- 对于每个旧节点,执行以下操作:
- 查找对应的新节点索引 newIndex:
- 如果旧节点有 key,通过 keyToNewIndexMap 获取 newIndex
- 如果没有 key,需要遍历新节点列表,找到第一个与旧节点相同的节点
- 判断节点是否存在与新节点列表:
- 如果 newIndex 没有找到,说明旧节点已经被删除,需要卸载
- 如果 newIndex 找到,说明节点需要保留,执行以下操作:
- 更新节点:调用 patch 函数更新节点内容
- 记录映射关系:将旧节点的索引 +1 记录到 `newIndexToOldIndexMap[newIndex - newStartIdx]` 中
>思考🤔:为什么要把旧节点的索引 +1 然后进行存储?
>
>答案:因为前面我们在初始化newIndexToOldIndexMap这个数组的时候,所有的值都初始化为了0,代表新节点在旧节点列表中不存在。如果直接存储旧节点的索引,而恰好这个旧节点的索引又为0,那么此时是无法区分究竟是索引值还是不存在。
- 标记节点是否需要移动:通过比较当前的遍历顺序和 newIndex,初步判断节点是否需要移动。
示意代码:
```js
let moved = false;
let maxNewIndexSoFar = 0;
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
const oldNode = oldChildren[i];
let newIndex;
if (oldNode.key != null) {
// 旧节点存在 key,根据 key 找到该节点在新节点列表里面的索引值
newIndex = keyToNewIndexMap.get(oldNode.key);
} else {
// 遍历新节点列表匹配
}
if (newIndex === undefined) {
// 旧节点在新节点中不存在,卸载
} else {
// 更新节点
patch(oldNode, newChildren[newIndex], container);
// 记录映射关系,注意这里在记录的时候,旧节点的索引要加1
newIndexToOldIndexMap[newIndex - newStartIdx] = i + 1;
// 判断是否需要移动
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
}
}
```
详细步骤:
- i = 0:`[0, 0, 0, 0, 1, 0]`
- i = 1:`[0, 2, 0, 0, 1, 0]`
- i = 2:`[0, 2, 3, 0, 1, 0]`
- i = 3::`[0, 2, 3, 4, 1, 0]`
之所以一开始初始化为 0 ,其实是为了一开始假设新节点不存在于旧节点列表,之后就会对这个数组进行更新,倘若更新之后当前某个位置还为 0 ,就代表这一位对应的新节点在旧节点列表中不存在。
**3. 更新newIndexToOldIndexMap**
遍历未处理的**旧节点**,查找旧节点在新节点中的位置,决定是更新、删除还是移动。
- 遍历未处理的旧节点(从 oldStartIdx 到 oldEndIdx)
- 对于每个旧节点,执行以下操作:
- 查找对应的新节点索引 newIndex:
- 如果旧节点有 key,通过 keyToNewIndexMap 获取 newIndex
- 如果没有 key,需要遍历新节点列表,找到第一个与旧节点相同的节点
- 判断节点是否存在与新节点列表:
- 如果 newIndex 没有找到,说明旧节点已经被删除,需要卸载
- 如果 newIndex 找到,说明节点需要保留,执行以下操作:
- 更新节点:调用 patch 函数更新节点内容
- 记录映射关系:将旧节点的索引 +1 记录到 `newIndexToOldIndexMap[newIndex - newStartIdx]` 中
>思考🤔:为什么要把旧节点的索引 +1 然后进行存储?
>
>答案:因为前面我们在初始化newIndexToOldIndexMap这个数组的时候,所有的值都初始化为了0,代表新节点在旧节点列表中不存在。如果直接存储旧节点的索引,而恰好这个旧节点的索引又为0,那么此时是无法区分究竟是索引值还是不存在。
- 标记节点是否需要移动:通过比较当前的遍历顺序和 newIndex,初步判断节点是否需要移动。
示意代码:
```js
let moved = false;
let maxNewIndexSoFar = 0;
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
const oldNode = oldChildren[i];
let newIndex;
if (oldNode.key != null) {
// 旧节点存在 key,根据 key 找到该节点在新节点列表里面的索引值
newIndex = keyToNewIndexMap.get(oldNode.key);
} else {
// 遍历新节点列表匹配
}
if (newIndex === undefined) {
// 旧节点在新节点中不存在,卸载
} else {
// 更新节点
patch(oldNode, newChildren[newIndex], container);
// 记录映射关系,注意这里在记录的时候,旧节点的索引要加1
newIndexToOldIndexMap[newIndex - newStartIdx] = i + 1;
// 判断是否需要移动
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
}
}
```
详细步骤:
- i = 0:`[0, 0, 0, 0, 1, 0]`
- i = 1:`[0, 2, 0, 0, 1, 0]`
- i = 2:`[0, 2, 3, 0, 1, 0]`
- i = 3::`[0, 2, 3, 4, 1, 0]`
 经过遍历旧节点列表这一操作之后,newIndexToOldIndexMap 就被更新,里面存储了每个新节点在旧节点列表里面的位置,不过要注意,这个索引位置是 +1. 更新后如果某一项仍然是 0,说明这一个节点确实在旧节点列表中不存在
```js
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
```
maxNewIndexSoFar 用于判断节点的相对顺序是否保持递增,以决定是否需要移动节点。
- 如果当前的新节点索引大于等于 maxNewIndexSoFar,更新 maxNewIndexSoFar,节点相对顺序正确,无需标记移动
- 如果小于,说明节点相对顺序发生变化,标记 moved = true,后续需要根据 LIS 决定是否移动节点。
**4. 计算最长递增子序列**
通过 LIS,确定哪些节点的相对顺序未变,减少需要移动的节点数量。如果在前面的步骤中标记了 moved = true,说明有节点需要移动。使用 newIndexToOldIndexMap 计算最长递增子序列 increasingNewIndexSequence.
```js
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : [];
```
上一步我们得到的 newIndexToOldIndex 为 `[0, 2, 3, 4, 1, 0]`,之后得到的最长递增子序列为 `[1, 2, 3]`,注意,Vue3内部在计算最长递增子序列的时候,返回的是元素对应的索引值。
思考🤔:注意这里的最长递增子序列不是记录的具体元素,而是元素对应的下标值。这样有什么好处?
答案:这样刚好抵消了前面+1的操作,重新变回了旧节点的下标。
**5. 移动和挂载节点**
根据计算结果,对需要移动和新建的节点进行处理。**倒序遍历**未处理的新节点。
思考🤔:为什么要倒序遍历?
答案:因为后续的节点位置是确定了的,通过倒序的方式能够避免锚点引用的时候不会出错。
具体步骤:
1. 计算当前新节点在新节点列表中的索引 newIndex = newStartIdx + i
- newStartIdx 是未处理节点的起始索引
- i 为倒序遍历时的索引值
2. 获取锚点 DOM,其目的是为了作为节点移动的参照物,当涉及到移动操作时,都移动到锚点 DOM 的前面
- 计算方法为 `newIndex + 1 < newChildren.length ? newChildren[newIndex + 1].el : null`
- 如果计算出来为 null,表示没有对应的锚点 DOM ,那么就创建并挂载到最后
3. 判断节点究竟是新挂载还是移动
- **判断节点是否需要挂载**:如果 `newIndexToOldIndexMap[i] === 0`,说明该节点在旧节点中不存在,需要创建并插入到锚点DOM位置之前。
```js
if (newIndexToOldIndexMap[i] === 0) {
// 创建新节点并插入到锚点DOM位置之前
patch(/*参数略 */);
}
```
- **判断节点是否需要移动**:如果节点在 increasingNewIndexSequence 中,说明位置正确,无需移动。如果不在,则需要移动节点到锚点DOM位置之前。
```js
else if (moved) {
if (!increasingNewIndexSequence.includes(i)) {
// 移动节点到锚点DOM之前
move(/*参数略 */);
}
}
```
详细步骤:
- i = 5
- newIndex = 5
- 锚点DOM:null
- 创建 m 对应的真实 DOM,挂载到最后
- i = 4
- newIndex = 4
- 锚点DOM:m --> 真实DOM
- `newIndexToOldIndexMap[4]` 是否为 0,不是说明在旧节点列表里面是有的,能够复用
- 接下来看 i 是否在最长递增子序列里面,发现没有在最长递增子序列里面,那么这里就涉及到移动,移动到锚点DOM的前面,也就是 m 前面
- i = 3
- newIndex = 3
- 锚点DOM:a --> 真实DOM
- `newIndexToOldIndexMap[3]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 2
- newIndex = 2
- 锚点DOM:d --> 真实DOM
- `newIndexToOldIndexMap[2]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 1
- newIndex = 1
- 锚点DOM:c --> 真实DOM
- `newIndexToOldIndexMap[1]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 0
- newIndex = 0
- 锚点DOM:b --> 真实DOM
- `newIndexToOldIndexMap[0]` 为0,说明旧节点列表里面没有
- 创建新的 DOM 节点,插入到锚点 DOM 节点之前
最终经过上面的操作:
1. e:新建并且插入到 b 之前
2. b: 位置不变,没有做移动操作
3. c:位置不变,没有做移动操作
4. d:位置不变,没有做移动操作
5. a:移动到 m 之前
6. m:新建并且插入到末尾
整个 diff 下来 DOM 操作仅仅有 1 次移动,2 次新建。做到了最最最小化 DOM 操作次数,没有一次 DOM 操作是多余的。
>面试题:讲一讲 Vue3 的 diff 算法做了哪些改变?
>
>参考答案:
>
>Vue2 采用的是双端 diff 算法,而 Vue3 采用的是快速 diff. 这两种 diff 算法前面的步骤都是相同的,先是新旧列表的头节点进行比较,当发现无法复用则进行新旧节点列表的尾节点比较。
>
>一头一尾比较完后,如果旧节点列表有剩余,就将对应的旧 DOM 节点全部删除掉,如果新节点列表有剩余:将新节点列表中剩余的节点创建对应的 DOM,放置于新头节点对应的 DOM 节点后面。
>
>之后两种 diff 算法呈现出不同的操作,双端会进行旧头新尾比较、无法复用则进行旧尾新头比较、再无法复用这是暴力比对,这样的处理会存在多余的移动操作,即便一些新节点的前后顺序和旧节点是一致的,但是还是会产生移动操作。
>
>而 Vue3 快速 diff 则采用了另外一种做法,找到新节点在旧节点中对应的索引列表,然后求出最长递增子序列,凡是位于最长递增子序列里面的索引所对应的元素,是不需要移动位置的,这就做到了只移动需要移动的 DOM 节点,最小化了 DOM 的操作次数,没有任何无意义的移动。可以这么说,Vue3 的 diff 再一次将性能优化到了极致,整套操作下来,没有一次 DOM 操作是多余的,仅仅执行了最必要的 DOM 操作。
---
-EOF-
经过遍历旧节点列表这一操作之后,newIndexToOldIndexMap 就被更新,里面存储了每个新节点在旧节点列表里面的位置,不过要注意,这个索引位置是 +1. 更新后如果某一项仍然是 0,说明这一个节点确实在旧节点列表中不存在
```js
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
```
maxNewIndexSoFar 用于判断节点的相对顺序是否保持递增,以决定是否需要移动节点。
- 如果当前的新节点索引大于等于 maxNewIndexSoFar,更新 maxNewIndexSoFar,节点相对顺序正确,无需标记移动
- 如果小于,说明节点相对顺序发生变化,标记 moved = true,后续需要根据 LIS 决定是否移动节点。
**4. 计算最长递增子序列**
通过 LIS,确定哪些节点的相对顺序未变,减少需要移动的节点数量。如果在前面的步骤中标记了 moved = true,说明有节点需要移动。使用 newIndexToOldIndexMap 计算最长递增子序列 increasingNewIndexSequence.
```js
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : [];
```
上一步我们得到的 newIndexToOldIndex 为 `[0, 2, 3, 4, 1, 0]`,之后得到的最长递增子序列为 `[1, 2, 3]`,注意,Vue3内部在计算最长递增子序列的时候,返回的是元素对应的索引值。
思考🤔:注意这里的最长递增子序列不是记录的具体元素,而是元素对应的下标值。这样有什么好处?
答案:这样刚好抵消了前面+1的操作,重新变回了旧节点的下标。
**5. 移动和挂载节点**
根据计算结果,对需要移动和新建的节点进行处理。**倒序遍历**未处理的新节点。
思考🤔:为什么要倒序遍历?
答案:因为后续的节点位置是确定了的,通过倒序的方式能够避免锚点引用的时候不会出错。
具体步骤:
1. 计算当前新节点在新节点列表中的索引 newIndex = newStartIdx + i
- newStartIdx 是未处理节点的起始索引
- i 为倒序遍历时的索引值
2. 获取锚点 DOM,其目的是为了作为节点移动的参照物,当涉及到移动操作时,都移动到锚点 DOM 的前面
- 计算方法为 `newIndex + 1 < newChildren.length ? newChildren[newIndex + 1].el : null`
- 如果计算出来为 null,表示没有对应的锚点 DOM ,那么就创建并挂载到最后
3. 判断节点究竟是新挂载还是移动
- **判断节点是否需要挂载**:如果 `newIndexToOldIndexMap[i] === 0`,说明该节点在旧节点中不存在,需要创建并插入到锚点DOM位置之前。
```js
if (newIndexToOldIndexMap[i] === 0) {
// 创建新节点并插入到锚点DOM位置之前
patch(/*参数略 */);
}
```
- **判断节点是否需要移动**:如果节点在 increasingNewIndexSequence 中,说明位置正确,无需移动。如果不在,则需要移动节点到锚点DOM位置之前。
```js
else if (moved) {
if (!increasingNewIndexSequence.includes(i)) {
// 移动节点到锚点DOM之前
move(/*参数略 */);
}
}
```
详细步骤:
- i = 5
- newIndex = 5
- 锚点DOM:null
- 创建 m 对应的真实 DOM,挂载到最后
- i = 4
- newIndex = 4
- 锚点DOM:m --> 真实DOM
- `newIndexToOldIndexMap[4]` 是否为 0,不是说明在旧节点列表里面是有的,能够复用
- 接下来看 i 是否在最长递增子序列里面,发现没有在最长递增子序列里面,那么这里就涉及到移动,移动到锚点DOM的前面,也就是 m 前面
- i = 3
- newIndex = 3
- 锚点DOM:a --> 真实DOM
- `newIndexToOldIndexMap[3]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 2
- newIndex = 2
- 锚点DOM:d --> 真实DOM
- `newIndexToOldIndexMap[2]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 1
- newIndex = 1
- 锚点DOM:c --> 真实DOM
- `newIndexToOldIndexMap[1]` 不为0,说明旧节点列表里面是有的,能够复用
- 接下来需要看 i 是否在最长递增子序列里面,发现存在,所以不做任何操作
- i = 0
- newIndex = 0
- 锚点DOM:b --> 真实DOM
- `newIndexToOldIndexMap[0]` 为0,说明旧节点列表里面没有
- 创建新的 DOM 节点,插入到锚点 DOM 节点之前
最终经过上面的操作:
1. e:新建并且插入到 b 之前
2. b: 位置不变,没有做移动操作
3. c:位置不变,没有做移动操作
4. d:位置不变,没有做移动操作
5. a:移动到 m 之前
6. m:新建并且插入到末尾
整个 diff 下来 DOM 操作仅仅有 1 次移动,2 次新建。做到了最最最小化 DOM 操作次数,没有一次 DOM 操作是多余的。
>面试题:讲一讲 Vue3 的 diff 算法做了哪些改变?
>
>参考答案:
>
>Vue2 采用的是双端 diff 算法,而 Vue3 采用的是快速 diff. 这两种 diff 算法前面的步骤都是相同的,先是新旧列表的头节点进行比较,当发现无法复用则进行新旧节点列表的尾节点比较。
>
>一头一尾比较完后,如果旧节点列表有剩余,就将对应的旧 DOM 节点全部删除掉,如果新节点列表有剩余:将新节点列表中剩余的节点创建对应的 DOM,放置于新头节点对应的 DOM 节点后面。
>
>之后两种 diff 算法呈现出不同的操作,双端会进行旧头新尾比较、无法复用则进行旧尾新头比较、再无法复用这是暴力比对,这样的处理会存在多余的移动操作,即便一些新节点的前后顺序和旧节点是一致的,但是还是会产生移动操作。
>
>而 Vue3 快速 diff 则采用了另外一种做法,找到新节点在旧节点中对应的索引列表,然后求出最长递增子序列,凡是位于最长递增子序列里面的索引所对应的元素,是不需要移动位置的,这就做到了只移动需要移动的 DOM 节点,最小化了 DOM 的操作次数,没有任何无意义的移动。可以这么说,Vue3 的 diff 再一次将性能优化到了极致,整套操作下来,没有一次 DOM 操作是多余的,仅仅执行了最必要的 DOM 操作。
---
-EOF-