243 lines
7.7 KiB
Markdown
243 lines
7.7 KiB
Markdown
# 浮点数精度问题
|
||
|
||
|
||
|
||
## 经典真题
|
||
|
||
|
||
|
||
- 为什么 *console.log(0.2+0.1==0.3)* 得到的值为 *false*
|
||
|
||
|
||
|
||
## 浮点数精度常见问题
|
||
|
||
|
||
|
||
在 *JavaScript* 中整数和浮点数都属于 *number* 数据类型,所有数字都是以 *64* 位浮点数形式储存,即便整数也是如此。 所以我们在打印 *1.00* 这样的浮点数的结果是 *1* 而非 *1.00* 。
|
||
|
||
在一些特殊的数值表示中,例如金额,这样看上去有点别扭,但是至少值是正确了。
|
||
|
||
然而要命的是,当浮点数做数学运算的时候,你经常会发现一些问题,举几个例子:
|
||
|
||
**场景一**:进行浮点值运算结果的判断
|
||
|
||
```js
|
||
// 加法
|
||
console.log(0.1 + 0.2); // 0.30000000000000004
|
||
console.log(0.7 + 0.1); // 0.7999999999999999
|
||
console.log(0.2 + 0.4); // 0.6000000000000001
|
||
console.log(2.22 + 0.1); // 2.3200000000000003
|
||
|
||
// 减法
|
||
console.log(1.5 - 1.2); // 0.30000000000000004
|
||
console.log(0.3 - 0.2); // 0.09999999999999998
|
||
|
||
// 乘法
|
||
console.log(19.9 * 100); // 1989.9999999999998
|
||
console.log(19.9 * 10 * 10); // 1990
|
||
console.log(9.7 * 100); // 969.9999999999999
|
||
console.log(39.7 * 100); // 3970.0000000000005
|
||
|
||
// 除法
|
||
console.log(0.3 / 0.1); // 2.9999999999999996
|
||
console.log(0.69 / 10); // 0.06899999999999999
|
||
```
|
||
|
||
|
||
|
||
**场景二**:将小数乘以 *10* 的 *n* 次方取整
|
||
|
||
比如将钱币的单位,从元转化成分,经常写出来的是 *parseInt(yuan\*100, 10)*
|
||
|
||
```js
|
||
console.log(parseInt(0.58 * 100, 10)); // 57
|
||
```
|
||
|
||
|
||
|
||
**场景三**:四舍五入保留 *n* 位小数
|
||
|
||
例如我们会写出 *(number).toFixed(2)*,但是看下面的例子:
|
||
|
||
```js
|
||
console.log((1.335).toFixed(2)); // 1.33
|
||
```
|
||
|
||
在上面的例子中,我们得出的结果是 *1.33*,而不是预期结果 *1.34*。
|
||
|
||
|
||
|
||
## 为什么会有这样的问题
|
||
|
||
|
||
|
||
似乎是不可思议。小学生都会算的题目,*JavaScript* 不会?
|
||
|
||
我们来看看其真正的原因,到底为什么会产生精度丢失的问题呢?
|
||
|
||
|
||
|
||
计算机底层只有 *0* 和 *1*, 所以所有的运算最后实际上都是二进制运算。
|
||
|
||
十进制整数利用辗转相除的方法可以准确地转换为二进制数,但浮点数呢?
|
||
|
||
|
||
|
||
<img src="https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/9fc493d0e2e84274b8445d8c5df405ae~tplv-k3u1fbpfcp-watermark.awebp" alt="img" style="zoom:50%;" />
|
||
|
||
|
||
|
||
*JavaScript* 里的数字是采用 *IEEE 754* 标准的 *64* 位双精度浮点数。
|
||
|
||
先看下面一张图:
|
||
|
||
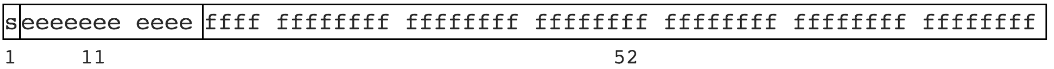
|
||
|
||
该规范定义了浮点数的格式,对于 *64* 位的浮点数在内存中的表示,最高的 *1* 位是符号位,接着的 *11* 位是指数,剩下的 *52* 位为有效数字,具体如下:
|
||
|
||
- 符号位 *S*:第 *1* 位是正负数符号位(*sign*),*0* 代表正数,*1* 代表负数
|
||
- 指数位 *E*:中间的 *11* 位存储指数(*exponent*),用来表示次方数
|
||
- 尾数位 *M*:最后的 *52* 位是尾数(*mantissa*),储存小数部分,超出的部分自动进一舍零
|
||
|
||
也就是说,浮点数最终在运算的时候实际上是一个符合该标准的二进制数
|
||
|
||
符号位决定了一个数的正负,指数部分决定了数值的大小,小数部分决定了数值的精度。
|
||
|
||
*IEEE 754* 规定,有效数字第一位默认总是 *1*,不保存在 *64* 位浮点数之中。也就是说,有效数字总是 *1.xx…xx* 的形式,其中 *xx…xx* 的部分保存在 *64* 位浮点数之中,最长可能为 *52* 位。因此,*JavaScript* 提供的有效数字最长为 *53* 个二进制位(*64* 位浮点的后 *52* 位 + 有效数字第一位的 *1*)。
|
||
|
||
既然限定位数,必然有截断的可能。
|
||
|
||
|
||
|
||
我们可以看一个例子:
|
||
|
||
```js
|
||
console.log(0.1 + 0.2); // 0.30000000000000004
|
||
```
|
||
|
||
为了验证该例子,我们得先知道怎么将浮点数转换为二进制,整数我们可以用除 *2* 取余的方式,小数我们则可以用乘 *2* 取整的方式。
|
||
|
||
|
||
|
||
*0.1* 转换为二进制:
|
||
|
||
*0.1 \* 2*,值为 *0.2*,小数部分 *0.2*,整数部分 *0*
|
||
|
||
*0.2 \* 2*,值为 *0.4*,小数部分 *0.4*,整数部分 *0*
|
||
|
||
*0.4 \* 2*,值为0.8,小数部分0.8,整数部分0
|
||
|
||
*0.8 \* 2*,值为 *1.6*,小数部分 *0.6*,整数部分 *1*
|
||
|
||
*0.6 \* 2*,值为 *1.2*,小数部分 *0.2*,整数部分 *1*
|
||
|
||
*0.2 \* 2*,值为 *0.4*,小数部分 *0.4*,整数部分 *0*
|
||
|
||
从 *0.2* 开始循环
|
||
|
||
|
||
|
||
*0.2* 转换为二进制可以直接参考上述,肯定最后也是一个循环的情况
|
||
|
||
|
||
|
||
所以最终我们能得到两个循环的二进制数:
|
||
|
||
*0.1:0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1100 ...*
|
||
|
||
*0.2:0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 ...*
|
||
|
||
这两个的和的二进制就是:
|
||
|
||
*sum:0.0100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 ...*
|
||
|
||
最终我们只能得到和的近似值(按照 *IEEE 754* 标准保留 *52* 位,按 *0* 舍 *1* 入来取值),然后转换为十进制数变成:
|
||
|
||
sum ≈ 0.30000000000000004
|
||
|
||
|
||
|
||
再例如:
|
||
|
||
```js
|
||
console.log((1.335).toFixed(2)); // 1.33
|
||
```
|
||
|
||
因为 *1.335* 其实是 *1.33499999999999996447286321199*,*toFixed* 虽然是四舍五入,但是是对 *1.33499999999999996447286321199* 进行四五入,所以得出 *1.33*。
|
||
|
||
|
||
|
||
在 *Javascript* 中,整数精度同样存在问题,先来看看问题:
|
||
|
||
```js
|
||
console.log(19571992547450991); // 19571992547450990
|
||
console.log(19571992547450991===19571992547450992); // true
|
||
```
|
||
|
||
|
||
|
||
同样的原因,在 *JavaScript* 中 *number* 类型统一按浮点数处理,整数是按最大 *54* 位来算,
|
||
|
||
- 最大( *2<sup>53</sup> - 1*,*Number.MAX_SAFE_INTEGER*、*9007199254740991*)
|
||
- 最小( *-(2<sup>53</sup> - 1)*,*Number.MIN_SAFE_INTEGER*、*-9007199254740991*)
|
||
|
||
所以只要超过这个范围,就会存在被舍去的精度问题。
|
||
|
||
|
||
|
||
当然这个问题并不只是在 *Javascript* 中才会出现,几乎所有的编程语言都采用了 *IEEE-754* 浮点数表示法,任何使用二进制浮点数的编程语言都会有这个问题。
|
||
|
||
只不过在很多其他语言中已经封装好了方法来避免精度的问题,而 *JavaScript* 是一门弱类型的语言,从设计思想上就没有对浮点数有个严格的数据类型,所以精度误差的问题就显得格外突出。
|
||
|
||
|
||
|
||
通常这种对精度要求高的计算都应该交给后端去计算和存储,因为后端有成熟的库来解决这种计算问题。
|
||
|
||
前端也有几个不错的类库:
|
||
|
||
|
||
|
||
***Math.js***
|
||
|
||
*Math.js* 是专门为 *JavaScript* 和 *Node.js* 提供的一个广泛的数学库。它具有灵活的表达式解析器,支持符号计算,配有大量内置函数和常量,并提供集成解决方案来处理不同的数据类型。
|
||
|
||
像数字,大数字(超出安全数的数字),复数,分数,单位和矩阵。 功能强大,易于使用。
|
||
|
||
|
||
|
||
***decimal.js***
|
||
|
||
为 *JavaScript* 提供十进制类型的任意精度数值。
|
||
|
||
|
||
|
||
***big.js***
|
||
|
||
不仅能够支持处理 *Long* 类型的数据,也能够准确的处理小数的运算。
|
||
|
||
|
||
|
||
## 真题解答
|
||
|
||
|
||
|
||
- 为什么 *console.log(0.2+0.1==0.3)* 得到的值为 *false*
|
||
|
||
> 参考答案:
|
||
>
|
||
> 因为浮点数的计算存在 *round-off* 问题,也就是浮点数不能够进行精确的计算。并且:
|
||
>
|
||
> - 不仅 *JavaScript*,所有遵循 *IEEE 754* 规范的语言都是如此;
|
||
> - 在 *JavaScript* 中,所有的 *Number* 都是以 *64-bit* 的双精度浮点数存储的;
|
||
> - 双精度的浮点数在这 *64* 位上划分为 *3* 段,而这 *3* 段也就确定了一个浮点数的值,*64bit* 的划分是“*1-11-52*”的模式,具体来说:
|
||
> - 就是 *1* 位最高位(最左边那一位)表示符号位,*0* 表示正,*1* 表示负;
|
||
> - *11* 位表示指数部分;
|
||
> - *52* 位表示尾数部分,也就是有效域部分
|
||
|
||
|
||
|
||
-*EOF*-
|
||
|
||
|